Detailed Description of the ICQMB Research Projects with UCR Departments, other Universities, National Laboratories and Medical Schools

 

Collaborative Projects

 

Integrative multiscale modeling and multimodal experiments to decode systems-level molecular mechanisms of epithelial systems

Collaborators: Dr. Mark Alber, Dr. Weitao Chen, Dr. Amit K. Roy Chowdhury (all UCR), Dr. Jeremy Zartman and Dr. Alexander Dowling (U Notre Dame)

This project seeks to combine mathematical modeling and experimentation to bridge the critical knowledge gaps required to predict how molecular signaling controlled by morphogens such as the Bone Morphogenetic Protein (BMP) and Wing-less/WNT signaling pathways through cytoskeletal regulators drives cell and tissue shape generation and maintenance during embryo development. Members of the team will integrate breakthroughs in mathematical theory of reaction-diffusion PDE systems on extending and deforming manifolds coupled with coarse graining mechanistic modeling approaches describing cell membrane and cytoskeleton with machine learning based surrogate models for image analysis, parameter estimation and uncertainty analysis.

 

Combined Modeling and Experimental Study of the Mechanisms of Growth Patterns in Stem Cell Homeostasis in Plants

Collaborators: Dr. Mark Alber, Dr. Weitao Chen, Dr. G. Venugopala Reddy and Dr. Amit K. Roy Chowdhury (all UCR)

This interdisciplinary research program aims to understand how mechanical connections among cells and chemical signals between them collaborate to control the growth, sell-organization and differentiation of stem cells during plant growth. Mathematical and computer models will allow researchers to perform virtual experiments that are currently impossible in the lab. Coupled with live imaging experiments and new image analysis methods, these experiments will yield insights into biological mechanisms governing organ formation in plants and animals and development of cancer in epithelial cell layers of the colon.

 

DOE/PNNL/ORNL-UCR project: Elucidating Principles of Bacterial-Fungal Interactions

Collaborators: Dr. Mark Alber (all UCR), Dr. William Cannon (PNNL) and Dr. Dale Pelletier (ORNL)

The focus of this project is the development hybrid machine learning/simulation models of Pseudomonas uorescens/Laccaria bicolor interactions and dynamics. These hybrid data-analytic/simulation models will be used to carry out virtual experiments and develop fundamental understanding of the interactions between Pseudomonas uorescens and Laccaria bicolor. A fundamental understanding of how a property emerges from underlying processes is developed through understanding how the physics of underlying processes result in the emergent property. For instance, how do changes in energy metabolism and signaling by chemoattractants result in the sophisticated chemotactic searches for food? At the same time, experiments will be carried out aimed at developing and testing quantitative assays to measure the same interactions, and whose data will inform the virtual experiments.

 

Collaborative project with University of Pennsylvania School of Medicine: Multi-scale mathematical modeling and empirical study of mechanisms limiting blood clot growth

Collaborators: Dr. Mark Alber, Dr. Zhiliang Xu (U Notre Dame) and Dr. John Weisel (UPenn)

Thrombosis is a major cause of death in the developed world and results from the growth of thrombi (blood clots forming within blood vessels) that restricts blood flow to vital organs. The project integrates multi-scale mathematical modeling and experiments to examine novel hypothesis related to the role of fibrin networks in processes halting thrombus growth. This will help physicians to estimate risk of thrombotic disease for an individual patient by identifying critical values of parameters of processes regulating thrombogenesis.

 

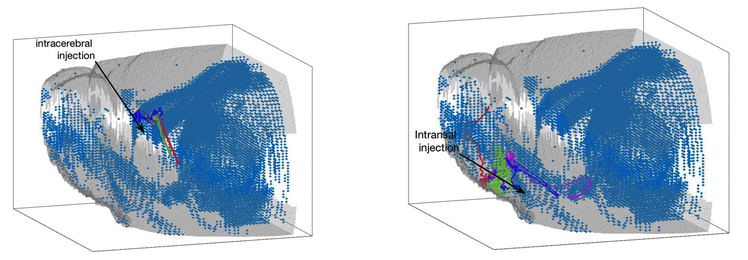
Collaborative project with City of Hope National Medical Center: mathematical modeling of chemotaxis-driven migration of therapeutic neural stem cells to sites of tumors and injury

Collaborators: Dr. Heyrim Cho, Dr. Russell Rockne (City of Hope), and Dr. Margarita Gutova (City of Hope)

Neural stem cells (NSC) have been shown to be a safe and effective means of treatment of primary brain tumors as well as traumatic brain injury. NSCs have demonstrated tropism to remote sites of tumor or injury in the brain, and have also been shown to migrate along anisotropic white matter tracts. NSCs may be delivered through several routes of administration, including intracerebral, intrathecal, and intranasal injection. This project aims to use mathematical modeling of chemotaxis-driven migration combined with anatomical features of the brain to predict--and subsequently improve--the efficiency of administration of NSCs to sites of tumor or injury. The models will be calibrated from pre-clinical animal models and compared with data collected from patients treated at City of Hope.

 

Collaborative project with City of Hope National Medical Center: mathematical modeling of hematopoiesis and leukemia from single-cell gene sequencing data

Collaborators: Dr. Heyrim Cho (UCR), Dr. Russell Rockne (City of Hope), and Dr. Ya-Huei Kuo (City of Hope)

Single-cell RNA sequencing data provides the gene expression level that is in the dimensionality of O(105) per each individual cell. By applying dimension reduction techniques, the data reveals a continuum of cell states that challenges the classical view of cell biology assuming discrete cell states. Continuum cell state models will be developed from single-cell RNA sequencing data to describe the trajectories in the continuum cell state space of hematopoiesis. The models will be used to study abnormal differentiation processes, e.g. acute myeloid leukemia progression, to predict the emergence of novel intermediate cell states, and used to investigate therapeutic targets.

 

Collaborative project with University of California, Irvine: Multi-Scale Modeling and Experimental Study of Hair Follicle Growth Control

Collaborators: Dr. Qixuan Wang (UCR), Dr. Maksim Plikus (UC Irvine)

Hair follicles are stem cell-rich skin mini-organs that can undergo oscillation-like cycles of regeneration throughout their lifetimes. In recent years, hair follicle has emerged as a leading model system for studying general mechanisms of stem cell control, tissue patterning during morphogenesis, regeneration and aging. Though powerful, traditional reductionist research approaches are limited by technological barriers and high experiment costs. This project aims to develop an interdisciplinary approach between computational modeling and experimentations to understand crucial questions that arise from the growth control of the follicle and stem cell lineage dynamics. It is anticipated that the new mathematical model developed in this project can be generalized to study multiple aspects of skin biology as well as other biological growth systems. (Supported by NSF DMS 1951184, DMS 1951144)

 

Interdisciplinary Investigation of Asthmatic Airway Remodeling

Collaborators: Dr. Qixuan Wang, Dr. Mark Alber (all UCR), Dr. Mona Eskandari (UCR, Mechanical Engineering, BREATHE Center)

Asthma is a serious health and socioeconomic issue all over the world, affecting more than 300 million individuals. In patients with asthma, the airway wall structure undergoes pathological modifications that include changes in the composition and organization of its cellular and molecular constituents, leading to the thickening and stiffening of the interstitial matrix in the innermost airway layer. These phenomena give rise to morphological remodeling resulting in lumen blockage. In this project, we develop multi-scale computational models to investigate the impact of fibrous network remodeling in asthma on the airway biomechanics and morphology. Model predictions are experimentally validated in Dr. Eskandari’s lab.

 

Underpinning Swimming Mechanisms of Eukaryotic Microorganisms via Computations and Analysis of PDEs

Collaborators: Dr. Qixuan Wang, Dr. Mykhailo Potomkin, Dr. Bhargav Rallabandi (UCR Mechanical Engineering)

At microscale, the main constituent of life on Earth is microorganisms. Examples are bacteria, spermatozoa, and other single-cell organisms. A biological cell typically uses flexible appendages, flagella and cilia, to propel itself in a fluidic environment. Flagellar beating is caused by activity of molecular motors (or so-called motor proteins) that bend the flagellum and result in life-like pulsating of the flagellum. In this project, we develop nonlinear PDE based multi-scale models that integrate molecular kinetics, flagellar beating and fluid-structure interaction. We also use techniques from numerical analysis, applied dynamical systems, elasticity and fluid dynamics to model and investigate the biophysical principles that lead to stable swimming dynamics of the cell.

 

Multidisciplinary University Research Initiative with University of Houston, University of Maryland, College Park, University of California, Los Angeles and Princeton University: Innovations in Mean-Field Game Theory for Scalable Computation and Diverse Applications

Collaborators: Dr. Wilfrid Gangbo (UCLA), Dr. Michele Gelfand (UMD) , Dr. Tom Goldstein  (UMD), Dr. Zhu Han (U Houston), Dr. Dana Nau (UMD), Dr.Stanley Osher (UCLA), Dr. H. Vincent Poor (Princeton), Dr. Yat Tin Chow (UCR), Dr. Wuchen Li (U South Carolina), Dr. Alpar Richard Meszaros (Durham U), Dr. Penghang Yin (SUNY), Dr. Micah Goldblum (UMD), Dr. Flavien Leger (ENS Paris), Dr. Matt Jacobs (UCLA), Dr. Karthik Elamvazhuthi (UCLA), Dr. Daniel McKenzie (UCLA), Dr. Chenchen Mou (CityU of HK), Dr. Levon Nurbekyan (UCLA), Dr. Brian Swenson (Princeton), Dr. Honglian Zhang (Princeton)

Mean field games study strategic decision making in large populations where the individual players with each other and each individual is affected only by certain averaged quantities of all the other individuals. The mean field represents the behavior of a large number of agents by their population density function. This setting connects with optimal transport theory, Nelson's stochastic mechanics, partial differential equations, optimization, probability and statistics with applications in machine learning problems. This project aims to have a coordinated effort based on an overarching mathematical framework, accurate modeling in diverse applications, and a set of algorithmic tools that support fast simulation, prediction, and inverse design for mean field game, and is a collaborative effort of partial differential equations, numerical analysis, optimization, machine learning, psychology, artificial intelligence and game theory, and electrical engineering.